Communications of the ACM

BLOG@CACM

Are My Requirements Complete?

By Bertrand Meyer
November 26, 2019
Comments (1)

Some important concepts of software engineering, established over the years, are not widely known in the community. One use of this blog is to provide tutorials on such overlooked ideas. My last article covered one pertaining to project management: the Shortest Possible Schedule property. Here is another, this time in the area of requirements engineering, also based on a publication that I consider to be a classic (it is over 40 years old) but almost unknown to practitioners.

Practitioners are indeed, as in most of my articles, the intended audience. I emphasize this point right at the start because if you glance at the rest of the text you will see that it contains (horror of horrors) some mathematical formulae, and might think "this is not for me". It is! The mathematics is very simple and my aim is practical: to shed light on an eternal question that faces anyone writing requirements (whatever the style, traditional or agile): how can I be sure that a requirements specification is complete?

To a certain extent you cannot. But there is better answer, a remarkably simple one which, while partial, helps.

Defining completeness

The better answer is called "sufficient completeness" and comes from the theory of abstract data types. It was introduced in a 1978 article by Guttag and Horning [1]. It is also implicit in a more down-to-earth document, the 1998 IEEE standard on how to write requirements [2].

There is nothing really new in the present article; in fact my book Object-Oriented Software Construction [3] contains an extensive discussion of sufficient completeness (meant to be more broadly accessible than Guttag and Horning's scholarly article). But few people know the concepts; in particular very few practitioners have heard of sufficient completeness (if they have heard at all of abstract data types). So I hope the present introduction will be useful. 

The reason the question of determining completeness of requirements seems hopeless at first is the natural reaction: complete with respect to what? To know that the specification is complete we would need a more general description of all that our stakeholders want and all the environment constraints, but this would only push the problem further: how do we know that such description itself is complete? 

That objection is correct in principle: we can never be sure that we did not forget something someone wanted, or some property that the environment imposes. But there also exist more concrete and assessable notions of completeness.

The IEEE standard gives three criteria of completeness. The first states that "all requirements" have been included, and is useless, since it  runs into the logical paradox mentioned above, and is tautological anyway (the requirements are complete if they include all requirements, thank you for the information!). The second is meaningful but of limited interest (a "bureaucratic" notion of completeness): every element in the requirements document is numbered, every cross-reference is defined and so on. The last criterion is the interesting one: "Definition of the responses of the software to all realizable classes of input data in all realizable classes of situations". Now this is meaningful. To understand this clause we need to step back to sufficient completeness and, even before that, to abstract data types.

Abstract data types will provide our little mathematical excursion (our formal picnic in the words of an earlier article) in our study of requirements and completeness. If you are not familiar with this simple mathematical theory, which every software practitioner should know, I hope you will benefit from the introduction and example. They will enable us to introduce the notion of sufficient completeness formally before we come back to its application to requirements engineering.

Specifying an abstract data type

 Abstract data types are the mathematical basis for object-oriented programming. In fact, OO programming but also OO analysis and OO design are just a realization of this mathematical concept at various levels of abstraction, even if few OO practitioners are aware of it. (Renewed reference to [3] here if you want to know more.)

An ADT (abstract data type) is a set of objects characterized not by their internal properties (what they are) but by the operations applicable to them (what they have), and the properties of these operations. If you are familiar with OO programming you will recognize that this is exactly, at the implementation level, what a class is. But here we are talking about mathematical objects and we do not need to consider implementation.

An example  of a type defined in this way, as an ADT, is a notion of POINT on a line. We do not say how this object is represented (a concept that is irrelevant at the specification level) but how it appears to the rest of the world: we can create a new point at the origin, ask for the coordinate of a point, or move the point by a certain displacement. The example is the simplest meaningful one possible, but it gives the ideas.

An ADT specification has three part: Functions, Preconditions and Axioms. Let us see them (skipping Preconditions for the moment) for the definition of the POINT abstract data type.

The functions are the operations that characterize the type. There are three kinds of function, defined by where the ADT under definition, here POINT, appears:

• Creators, where the type appears only among the results.
• Queries, where it appears only among the arguments.
• Commands, where it appears on both sides.

There is only one creator here:

new: → POINT

new is a function that takes no argument, and yields a point (the origin). We will write the result as just new (rather than using empty parentheses as in new ()).

Creators correspond in OO programming to constructors of a class (creation procedures in Eiffel). Like constructors, creators may have arguments: for example instead of always creating a point at the origin we could decide that new creates a point with a given coordinate, specifying it as INTEGER → POINT and using it as new (i) for some integer i (our points will have integer coordinates). Here for simplicity we choose a creator without arguments. In any case the new type, here POINT, appears only on the side of the results.

Every useful ADT specification needs at least one creator, without which we would never obtain any objects of the type (here any points) to work with.

There is also only one query:

x: POINT → INTEGER

 which gives us the position of a point, written x (p) for a point p. More generally, a query enables us to obtain properties of objects of the new type. These properties must be expressed in terms of types that we have already defined, like INTEGER here. Again there has to be at least one query, otherwise we could never obtain usable information (information expressed in terms of what we already know) about objects of the new type. In OO programming, queries correspond to fields (attributes) of a class and functions without side effects.

And we also have just one command:

move: POINT × INTEGER → POINT

a function that for any point p and integer i and yields a new point, move (p, i).  Again an ADT specification is not interesting unless it has at least one command, representing ways to modify objects. (In mathematics we do not actually modify objects, we get new objects. In imperative programming we will actually update existing objects.) In the classes of object-oriented programming, commands correspond to procedures (methods which may change objects).

You see the idea: define the notion of POINT through the applicable operations.

Listing their names and the types of their arguments types results (as in POINT × INTEGER → POINT) is not quite enough to specify these operations: we must specify their fundamental properties, without of course resorting to a programming implementation. That is the role of the second component of an ADT specification, the axioms.

For example I wrote above that new yields the origin, the point for which x = 0,  but you only had my word for it. My word is good but not good enough. An axiom will give you this property unambiguously:

x (new) = 0                                    -- A0

The second axiom, which is also the last, tells us what move actually does. It applies to any point p and any integer m:

x (move (p, m)) = x (p) + m       -- A1

In words: the coordinate of the point resulting from moving p by m is the coordinate of p plus m.

That's it! (Except for the notion of precondition, which will wait a bit.) The example is trivial but this approach can be applied to any number of  data types, with any number of applicable operations and any level of complexity. That is what we do, at the design and implementation level, when writing classes in OO programming.

Is my ADT sufficiently complete?

Sufficient completeness is a property that we can assess on such specifications. An ADT specification for a type T (here POINT) is sufficiently complete if the axioms are powerful enough to yield the value of any well-formed query expression in a form not involving T. This definition contains a few new terms but the concepts are very simple; I will explain what it means through an example.

With an ADT specification we can form all kinds of expressions, representing arbitrarily complex specifications. For example:

x (move (move (move (new, 3), x (move (move (new, -2), 4))), -6))

This expression will yield an integer (since function x has INTEGER as its result type) describing the result of a computation with points. We can visualize this computation graphically; note that it involves creating two points (since there are two occurrences of new) and moving them, using in one case the current coordinate of one of them as displacement for the other. The following figure illustrates the process.

 

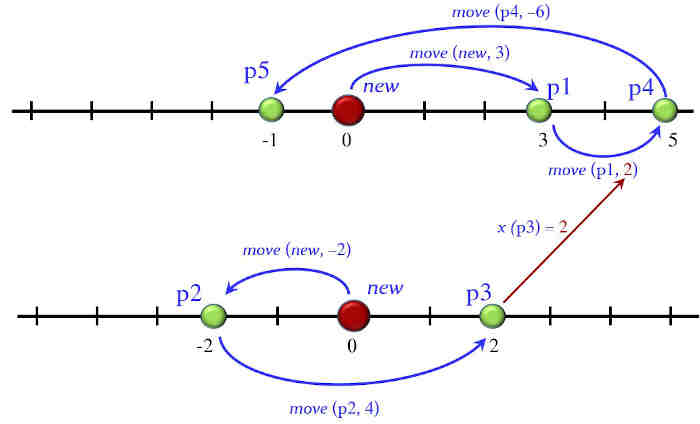
The result, obtained informally by drawing this picture, is the x of P5, that is to say -1. We will derive it mathematically below.

Alternatively, if like most programmers (and many other people) you find it more intuitive to reason operationally than mathematically, you may think of the previous expression as describing the result of the following OO program (with variables of type POINT):

create p                                -- In C++/Java syntax: p = new POINT();
create q
p.move (3)
q.move (-2)
q.move (4)
p.move (q.x)
p.move (-6)

Result := p.x

You can run this program in your favorite OO programming language, using a class POINT with new, x and move, and print the value of Result, which will be -1.

Here, however, we will stay at the mathematical level and simplify the expression using the axioms of the ADT, the same way we would compute any other mathematical formula, applying the rules without needing to rely on intuition or operational reasoning. Here is the expression again (let's call it i, of type INTEGER):

i = x (move (move (move (new, 3), x (move (move (new, -2), 4))), -6))

A query expression is one in which the outermost function being applied, here x, is a query function. Remember that a query function is one which the new type, here POINT, appears only on the left. This is the case with x, so the above expression i is indeed a query expression.

For sufficient completeness, query expressions are the ones of interest because their value is expressed in terms of things we already know, like INTEGERs, so they are the only way we can concretely obtain directly usable information the ADT (to de-abstract it, so to speak).

But we can only get such a value by applying the axioms. So the axioms are "sufficiently complete" if they always give us the answer: the value of any such query expression.

 Let us see if the above expression i satisfies this condition of sufficient completeness. To make it more tractable let us write it in terms of simpler expressions (all of type POINT), as illustrated by the figure below:

p1 = move (new, 3)
p2= move (new, -2)
p3= move (p2, 4)
p4= move (p1, x (p3))
p5= move (p4, -6)
i = x (p5)

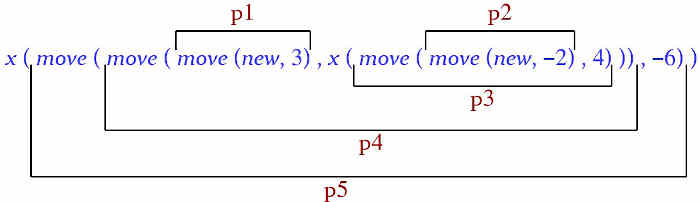
(You may note that the intermediate expressions roughly correspond to the steps in the above interpretation of the computation as a program. They also appear in the illustrative figure repeated next.)

 

Now we start applying the axioms to evaluating the expressions. Remember that we have two axioms: A0 tells us that x (new) = 0 and A1 that x (move (p, m)) = x (p) + m. Applying A1 to the definition the expression i yields

i = x (p4) - 6
  = i4 - 6  

if we define

i4 = x (p4)      -- Of type INTEGER

We just have to compute i4. Applying A1 to the definion of p4 tells us that

i4 = x (p1) + x (p3)

To compute the two terms:

• Applying A1 again, we see that the first term x (p1) is x (new) + 3, but then A0 tells us that x (new) is zero, so x (p1) is 3.
• As to x (p3), it is, once more from A1, x (p2) + 4, and x (p2) is (from A1 then A0), just -2, so x (p3) is 2.

In the end, then, i4 is 5, and the value of the entire expression i = i4 - 6 is -1. Good job!

Proving sufficient completeness

The successful computation of i was just a derivation for one example, showing that in that particular case the axioms yield the answer in terms of an INTEGER. How do we go from one example to an entire specification?

The bad news first: like all interesting problems in programming, sufficient completeness of an ADT specification is theoretically undecidable. There is no general automatic procedure that will process an ADT specification and print out "sufficiently complete" or "not sufficiently complete".

Now that you have recovered from the shock, you can share the computer scientist's natural reaction to such an announcement: so what. (In fact we might define the very notion of computer scientist as someone who, even before he brushes his teeth in the morning -- if he brushes them at all -- has already built the outline of a practical solution to an undecidable problem.) It is enough that we can find a way to determine if a given specification is sufficiently complete. Such a proof is, in fact, the computer scientist's version of dental hygiene: no ADT is ready for prime time unless it is sufficiently complete.

The proof is usually not too hard and will follow the general style illustrated for our simple example.

We note that the definition of sufficient completeness said: "the axioms are powerful enough to yield the value of any well-formed query expression in a form not involving the type". I have not defined "well-formed" yet. It simply means that the expressions are properly structured, with the proper syntax (basically the correct matching of parentheses) and proper number and types of arguments. For example the following are not well-formed (if p is an expression of type POINT):

move (p, 55(     -- Bad use of parentheses.
move (p)            -- Wrong number of arguments.
move (p, p)       -- Wrong type: second argument should be an integer.

Such expressions are nonsense, so we only care about well-formed expressions. Note that in addition to new, x and move , an expression can use integer constants as in the example (although we could generalize to arbitrary integer expressions). We consider an integer constant as a query expression.

We have to prove that with the two axioms A0 and A1 we can determine the value of any query expression i. Note that since the only query functions is x, the only possible form for i, other than an integer constant, is x (p) for some expression p of type POINT.

The proof proceeds by induction on the number n of parenthesis pairs in a query expression i.

There are two base steps:

• n = 0: in that case i can only be an integer constant. (The only expression with no parentheses built out of the ADT's functions is new, and it is not a query expression.) So the value is known. In all other cases i will be of the form x (p) as noted.
• n = 1: in that case p  can only be new, in other words i = x (new), since the only function that yields points, other than new, is move, and any use of it would add parentheses. In this case axiom A0 gives us the value of i: zero.

For the induction step, we consider i with n + 1 parenthesis pairs for n > 1. As noted, i is of the form x (p), so p has exactly n parenthesis pairs. p cannot be new (which would give 0 parenthesis pairs and was taken care of in the second base step), so p has to be of the form

p =  move (p', i')    -- For expressions p' of type POINT and i' of type INTEGER.

implying (since i = x (p)) that by axiom A1, the value of i is

x (p') + i'

So we will be able to determine the value of i if we can determine the value of both x (p') and i'. Since p has n parenthesis pairs and p =  move (p', i'), both p' and i' have at most n - 1 parenthesis pairs. (This use of n - 1 is legitimate because we have two base steps, enabling us to assume n > 1.) As a consequence, both x (p') and i' have at most n parenthesis pairs, enabling us to deduce their values, and hence the value of i, by the induction hypothesis.

Most proofs of sufficient completeness in my experience follow this style: induction on the number of parenthesis pairs (or the maximum nesting level).

Preconditions

I left until now the third component of a general ADT specification: preconditions. The need for preconditions arises because most practical specifications need some of their functions to be partial. A partial function from X to Y is a function that may not yield a value for some elements of X. For example, the inverse function on real numbers, which yields 1 / a for x, is partial  since it is not defined for a = 0 (or, on a computer, for non-zero but very small a).

Assume that in our examples we only want to accept points that lie in the interval [-4, +4]:

 

 We can simply model this property by turning move into a partial function. It was specified above as

move: POINT × INTEGER → POINT

The ordinary arrow → introduces a total (always defined) function. For a partial function we will use a crossed arrow -|->, specifying the function [4] as

move: POINT × INTEGER -|-> POINT

Other functions remain unchanged. Partial functions cause trouble: for f in X -|-> Y we can no longer cheerfully use f (x) if f is a partial function, even for x of the appropriate type X. We have to make sure that x belongs to the domain of f, meaning the set of values for which f is defined. There is no way around it: if you want your specification to be meaningful and it uses partial functions, you must specify explicitly the domain of each of them. Here is how to do it, in the case of move:

move (p: POINT; d: INTEGER) require |x (p) + d | < 5    -- where |...| is absolute value

To adapt the definition (and proofs) of sufficient completeness to the possible presence of partial functions:

• We only need to consider (for the rule that axioms must yield the value of query expressions) well-formed expressions that satisfy the associated preconditions.
• The definition must, however, include the property that axioms always enable us to determine whether an expression satisfies the associated preconditions (normally a straightforward part of the proof since preconditions are themselves query expressions).

Updating the preceding proof accordingly is not hard.

Back to requirements

The definition of sufficient completeness is of great help to assess the completeness of a requirements document. We must first regretfully note that for many teams today requirements stop at  "use cases" (scenarios) or  "user stories". Of course these are not requirements; they only describe individual cases and are to requirements what tests are to programs. They can serve to check requirements, but do not suffice as requirements. I am assuming real requirements, which include descriptions of behavior (along with other elements such as environment properties and project properties). To describe behaviors, you will define operations and their effects. Now we know what the old IEEE standard is telling us by stating that complete requirements should include

definition of the responses of the software to all realizable classes of input data in all realizable classes of situations

Whether or not we have taken the trouble to specify the ADTs, they are there in the background; our system's operations reflect the commands, and the effects we can observe reflect the queries. To make our specification complete, we should draw as much as possible of the (mental or explicit) matrix of possible effects of all commands on all queries. "As much as possible" because software engineering is engineering and we will seldom be able to reach perfection. But the degree of fullness of the matrix tells us a lot (possible software metric here?) about how close our requirements are to completeness.

I should note that there are other aspects to completeness of requirements. For example the work of Michael Jackson, Pamela Zave and Axel van Lamsweerde (more in some later article, with full references) distinguishes between business goals, environment constraints and system properties, leading to a notion of completeness as how much the system properties meet the goals and obey the constraints [5]. Sufficient completeness operates at the system level and, together with its theoretical basis, is one of those seminal concepts that every practicing software engineer or project manager should master.

Bertrand Meyer is chief technology officer of Eiffel Software (Goleta, CA), professor and provost at the Schaffhausen Institute of Technology (Switzerland), and head of the software engineering lab at Innopolis University (Russia).

 

References and notes

[1] John V. Guttag, Jim J. Horning: The Algebraic Specification of Abstract Data Types, in Acta Informatica, vol. 10, no. 1, pages 27-52, 1978, available here from the Springer site. This is a classic paper but I note that few people know it today; in Google Scholar I see over 700 citations but less than 100 of them in the past 8 years.

[2]  IEEE: Recommended Practice for Software Requirements Specifications, IEEE Standard 830-1998, 1998. This standard is supposed to be obsolete and replaced by newer ones, more detailed and verbose, but it remains the better reference: plain, modest and widely applied by the industry. It does need an update, but a good one.

[3] Bertrand Meyer, Object-Oriented Software Construction, 2nd edition, Prentice Hall, 1997. The discussion of sufficient completeness was in fact already there in the first edition from 1988.

[4] There is a nice HTML crossed-arrow character, &#8696;, but CACM's blog-writing software does not process it correctly, so we'll make do with -|->

[5] With thanks to Elisabetta Di Nitto from Politecnico di Milano for bringing up this notion of requirements completeness.

 

---

Comments

---

Displaying 1 comment