Communications of the ACM
How Does One Multiply with Napier's Rods?

Napier's rods, also called Napier's bones (see Fig. 1), were invented at the beginning of the 17th century. They have been used for multiplication and division until the 19th century. There were various forms, e.g. rotating cylinders.

This calculating aid introduced by Scottish mathematician John Napier in 1617 simplifies multiplication and division.
The basic multiplication table is printed on each of the four sides of the wooden rods.
Here, J stands for the numeral 1. For calculations, the rods were placed next to each other.
The procedure is based on the lattice method ("gelosia").
Credit: ETH Zurich, Collection of astronomical instruments
Instructions for Using Napier's Bones
Napier's multiplication and division rods, deriving from the basic multiplication table, simplify calculations considerably. They were also built into several mechanical calculating aids as rotating drums. The intermediate results are read from the diagonal grid and added by hand, taking account of the tens carry. According to the model, the diagonals run from the lower left to the upper right or from the upper left to the lower right. The tens are at the upper left or the lower left, respectively, and the ones at the lower right or the upper right, respectively.
Multiplication
Example 1: 7 × 694,387 = 4,860,709 (see Fig. 2)
Example 2: 7152 × 694,387 = 4,966,255,824 (see Fig. 3)
- Lay the rods with the numerals of the multiplicand next to each other. Place the rod with the (single-digit) multiplier (numerals 1 to 9) to the left of these.
- Read out the result of the multiplication directly from row 7 (the multiplier): 4, 2 + 6, 3 + 2, 8 + 2, 1 + 5, 6 + 4, 9.
Taking account of the tens carry (from right to left) gives the numbers:4, 8, 6, 0, 7,0, 9.
The product is then 4,860,709.
With a multi-digit multiplier, the partial products for the individual numbers are read off in the same way and then added, in each case shifted by one decimal place.
Napier's bones
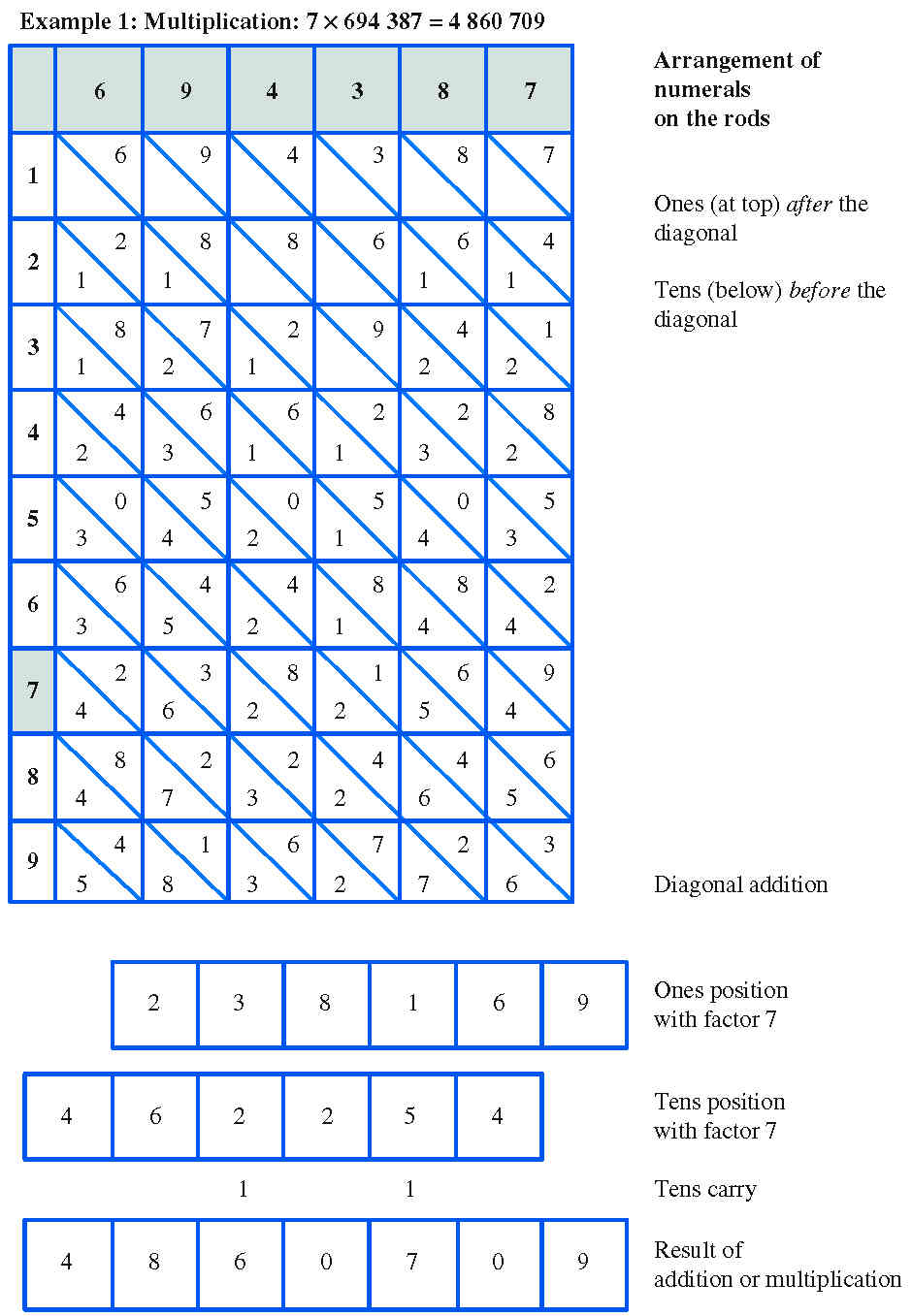
The calculation is imagined as a drawing. In this example, the multiplier has only one digit.
Credit: Bruderer Informatik, CH-9401 Rorschach, Switzerland
Napier's bones
In this example, both factors, the multiplicand and the multiplier, are multi-digit numbers.
Credit: Bruderer Informatik, CH-9401 Rorschach, Switzerland
Source
Bruderer, Herbert: Milestones in Analog and Digital Computing, Springer Nature Switzerland AG, Cham, 3rd edition 2020, 2 volumes, 2113 pages, 715 illustrations, 151 tables, https://www.springer.com/de/book/9783030409739 (translated by Dr. John McMinn)
Herbert Bruderer is a retired lecturer in didactics of computer science at ETH Zurich. More recently, he has been an historian of technology. [email protected], herbert.bruderer@bluewin.
No entries found